Skip to main content

数据结构与算法基本概念​

什么是数据结构？​

  • 数据结构指的相互之间有一种或多种特定关系的数据元素集合。
  • 计算机在对数据进行存储时候并不是杂乱没有顺序的，而是具有一定的规则。
  • 数据结构可以分成逻辑结构和物理结构。

逻辑结构​

抽象意义上的结构，按照对象中元素的关系分类。

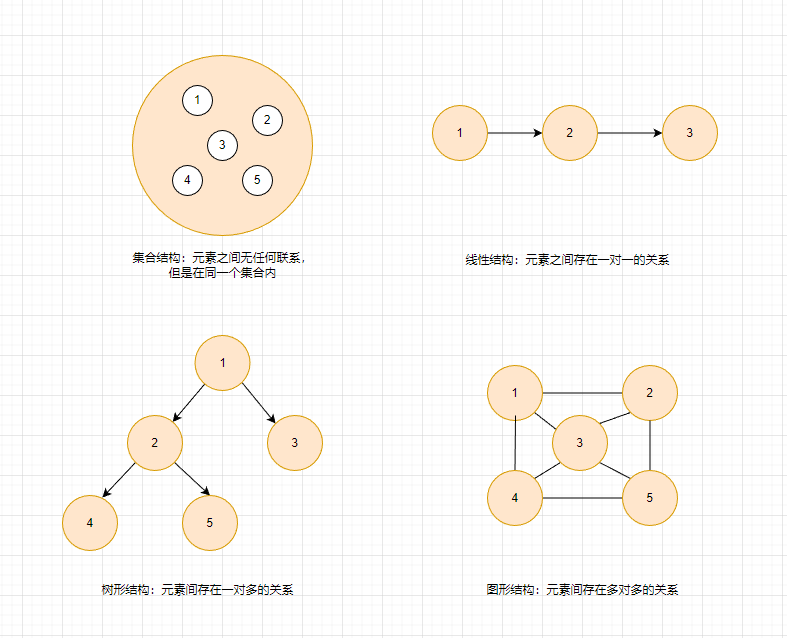
image-20230102211537785

物理结构​

又叫存储结构，主要有顺序存储跟链式存储。

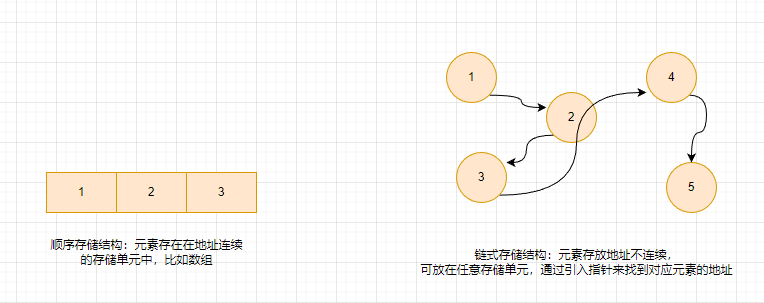
image-20230102212942238

什么是算法？​

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。

大白话：在一定的条件下，对数据进行计算，经过不断的优化，选择最合适的一种计算方式，以最快的方式得到需要的结果。

程序 = 数据结构+算法​

在计算机里来说，如果把单独的数据结构和算法拿出来讨论其实意义不大，就像鱼离不开水，算法也离不开数据结构。如果数据之间没有任何结构的话，算法也就无法实现了，毫无意义了。当然即使数据之间有关系，但是不对这些数据进行操作的话也没啥意义。

时间复杂度​

研究算法的最终目的就是怎么样花费更少的时间与内存来完成需求，不同的算法之间消耗的时间和空间会存在差异。

关于对算法时间耗费分析，称之为时间复杂度分析。

对程序的执行时间的分析有两种方法​

事后统计法​

  • 把程序运行起来，把所消耗的时间统计起来进行分析比较，这一些方法是可行的，但是会有一些问题：
  • 第一，要对设计的算法性能进行评测的话需要运行该程序。
  • 第二，就是所得的时间统计会依赖硬件、软件等等环境因素，这一种方式，需要在相同计算机下相同状态运行。这才能比较哪一个算法快。

事前估算法​

通过时间复杂度来判断哪一个算法更优。

时间频度T(n)​

  • 一个算法所花费的时间跟算法中里语句的执行次数是成正比的。
  • 算法里的执行次数越多，说明所消耗的时间就越多。
  • 一个算法中语句执行的次数被称为时间频度T(n)。
// 计算1-10000的和
public static void main(String[] args) {
    // for循环累加
    int sum=0;
    for(int i=1;i<=10000;i++){
        sum+=i;
    }
    System.out.println("1-10000的和为"+sum);
    
    // 1+10000=10001,2+9999=10001,共有5000对，得出公式(1+n)*n/2
    int sum2;
    sum2=(1+10000)*10000/2;
    System.out.println("1-10000的和为"+sum2);
}

// 使用for循环来进行计算，可以得出第一种的时间频度就是T(n)=n+1;n为执行次数，1是最后面还要执行一次。
// 直接进行计算，时间频度为T(n)=1。
// 当n的规模变大，则时间频度也会变大。
// 注意：算法函数中的常数项、低次项、系数可以忽略。
// 如：T(n)=n+10；10为常数项可以忽略，T(n)=n。
// T(n)=n^2+2n+10； 2n为低次项和10可以忽略，T(n)=2n。

使用大O计数法表示时间复杂度​

  • 算法的时间复杂度通常用大O符号来表示，定义的形式为T[n]=O(f(n))，称T(n)受限于f(n)。
  • 如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)，T(n)是关于问题规模n的函数。
  • T(n)称为这一算法的“时间复杂度”。当输入量n逐渐加大时，时间复杂度的极限情形称为算法的“渐进时间复杂度”。

常见的时间复杂度-使用大O阶表示​

常数阶O(1)​

// 这个代码不管是执行了多少次，只要没有循环等复杂的结构，那么时间复杂度就是O(1)
public static void main(String[] args) {
    int a=0;
    ++a;
    int c=a+1;
}

线性阶O(n)​

// 这段代码for循环里面的语句会执行n次，因为随着n的变化所消耗的时间也会随着变化，这类的代码都可以用O(n)来表示。
public static void main(String[] args) {
    int sum= 0;
    for(int i =1;i<=100;i++){
        sum+=i;
    }
}

平方阶O(n²)​

// 这段代码n是10，外层循环执行10次，内层循环执行10次，总共执行10*10=100次，也就是n的平方次，使用O(n^2)来表示。
// 同理，如果使用了三层for循环，那么时间复杂度就为O(n^3)立方阶。
public static void main(String[] args) {
     int sum= 0;
     int n=10;
     for(int j = 1;j<=n;j++){
         for(int i =1;i<n;i++){
             sum+=i;
         }
     }
     System.out.println(sum);
 }

²

对数阶O(Logn)​

补充：如果a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数（logarithm），记作x=logₐN。其中，a叫做对数的底数，N叫做真数。 

// 这里的while循环，每经过一轮，也就是每经过一次i=i*2的运算，结果i就离sum的值越近，也就是2*x=n;时间复杂度就是O(Logn)。
public static void main(String[] args) {
    int i=1;
    int sum=100;
    while(i<sum){
        i=i*2;
    }
}

常见算法时间复杂度排序由小到大​

O(1)<O(Logn)<O(n)<O(nlog₂n)<O(n²)<O(n³)<O(nᵏ)<O(2ⁿ)<O(n!)<O(nⁿ)，随着规模n的不断变大，执行的效率就越低。

平均时间复杂度与最坏时间复杂度​

  • 平均时间复杂度说的是任何的算法时间复杂度都是O(n²)。
  • 最坏情况时间复杂度指的是每次都是查到最后一个才是期望数字O(n²)。

空间复杂度​

  • 类似时间复杂度，一个算法的空间复杂度定义应该是该算法所消耗的存储空间。
  • 空间复杂度主要是对一个算法在运行时占用存储空间的量度，在做算法分析时，主要是讨论时间复杂度，因为从用户使用来看，更看重的是程序的速度。

常见算法问题​

字符串匹配问题​

  • 有一个字符串 str1= "BBCABCDAB ABCDABCDABDE"，和一个子串 str2="ABCDABD"；
  • 现在要判断 str1 是否含有 str2, 如果存在，就返回第一次出现的位置, 如果没有，则返回-1。

第一种方法：暴力匹配法​

第二种方法：KMP算法​

八皇后问题​

线性结构与非线性结构​

什么是线性结构​

  • 线性结构是最常用的数据结构，它的特点是数据元素之间是一对一的关系，如数组a[0]=1，那么数组下标为0的时候就等于1了，这就是一对一的关系。
  • 线性结构的储存结构有两种，一种是顺序存储结构（以数组方式），一种是链式存储结构（链表）。
  • 顺序存储结构的线性表又被称为顺序表，顺序表里存储的元素是连续的，分配的地址也是连续的。
  • 链式存储的线性表又被称为链表，链表里存储的元素不一定是连续的，一般所存储的数据作为一个节点，每个节点分配一个指针来找到下一个节点的位置获取相关信息。
  • 线性结构常见的有：数组、队列、栈、链表。

什么是非线性结构​

  • 非线性结构里的各个数据元素不保持在一个线性的序列当中，每个数据元素都可能会与0个或多个其他的数据元素发生联系。
  • 非线性结构常见的有：二维（多维）数组、广义表、树结构、图结构。

线性表的基本概念​

什么是线性表​

  • 两个元素有“一对一”逻辑关系的数据，其储存方式就是线性表。
  • 线性表也叫线性储存结构，是基本最常用的一种数据结构，由n个具有相同特性的数据元素组成的序列。
  • 线性表储存数据就是把所有的数据用一根线穿起来，放到物理空间中，数据依次存储到物理空间，就称为顺序表，数据分散存放的结构也称为链表。

线性表

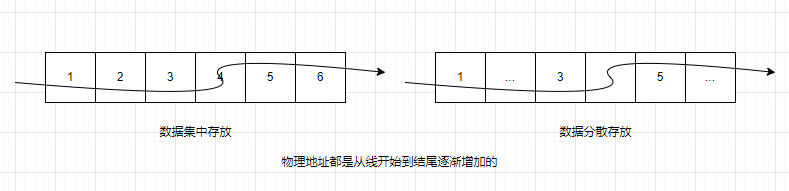
线性表相关术语​

  • 线性表中的每个个体被称为数据元素，图中1、2、3都是一个元素。
  • 具有一对一逻辑关系的数据。
  • 某个元素左边的相邻元素称为前驱元素，右边的相邻元素称为后继元素，如图4的前驱元素和后继元素。

线性表相关术语

总结线性表的特征​

  • 数据元素之间具有一对一的关系。
  • 第一个元素没有前驱元素，如图1，这个1也被称为头元素。
  • 最后一个元素没有后继元素，图图6，这个6也被称为尾元素。
  • 除了头元素跟尾元素，其他元素只存在一个前驱或者后继节点。

什么是顺序表​

  • 顺序表是用一段物理地址连续的储存单元进行储存元素的线性结构，通常是以数组进行存储。
  • 通过数据元素物理储存的相邻关系来反映数据元素之间逻辑上的相邻关系。

顺序表-数组

顺序表简介初始化和判空判满功能实现​

顺序表一般包含的几种方法​

判断顺序表是否满public boolean isEmpty()
判断顺序表是否为空表public boolean isFull()
向顺序表中添加元素public void add(int ele)
删除指定位置的元素public void del(int ele)
在指定的位置添加元素public void insert(int i, int ele)
修改数据public void changeData(int i, int ele)
获取顺序表的长度public int getLength()
获取对应位置的元素public int getNum(int i)
遍历输出顺序表public void showNum()

代码实现顺序表的初始化以及判空判满​